Capacitors in series are capacitors that are connected one after the other. The result always becomes a capacitance that is lower than the lowest value.
In this guide, you’ll learn why this is the case and how to calculate their combined values. And I’ll also throw in a simple rule of thumb that you can use when you don’t have a calculator at hand. So let’s dive in!
Why Do You Get A Lower Value?
When you connect capacitors in series, you connect them one after the other. And you can think of them as one capacitor with a value that is always lower than the lowest value.
For example, if you connect three 300 µF in series, the combined capacitance becomes 100 µF. This can be useful for getting a specific capacitor value that you don’t currently have in your component selection.
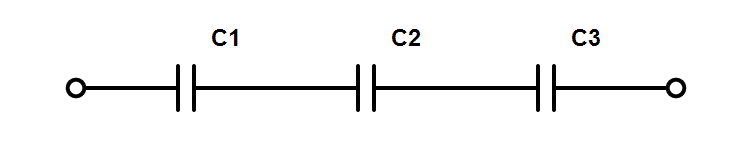
The fact that the capacitance becomes lower as you add more capacitors sounds counterintuitive at first.
But when you think of how capacitors work, it starts to make sense: A capacitor is basically just two metallic plates, placed close to each other, with an insulating material in between.
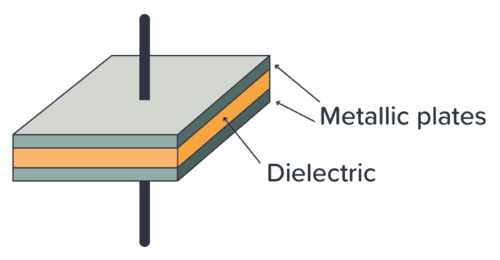
The larger the space between the plates, the lower the capacitance. So when you place two (or more) capacitors in series, you get more space between the first and last plates. And the capacitance gets lower.
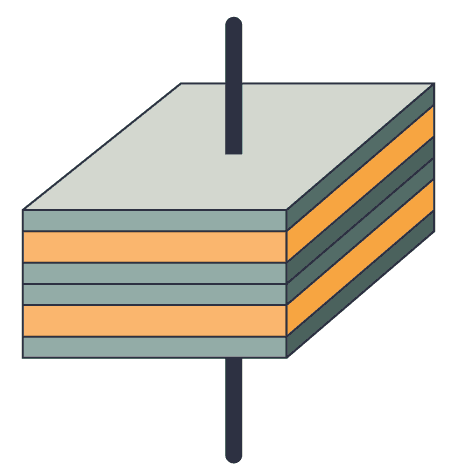
How to Calculate the Value of Capacitors in Series
Calculating capacitors in series is done in the same way as you calculate resistors in parallel.

Get Our Basic Electronic Components Guide
Learn how the basic electronic components work so that circuit diagrams will start making sense to you.
This is the formula for calculating the total capacitance of three capacitors connected in series:
![]()
To find CTOTAL you need to flip both sides, and you’ll end up with this:
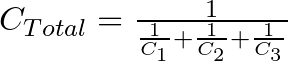
This is a little bit less intuitive than calculating capacitors in parallel.
But if you use the same value for all the capacitors that you place in series, the calculation becomes easy. The resulting value becomes the value of one, divided by the number of capacitors. So if you for example place three 330 nF capacitors in series, you’ll end up with 330 nF / 3 = 110 nF.
You can place as many capacitors in series as you want. Just add more C’s to the formula above.
Example Calculation
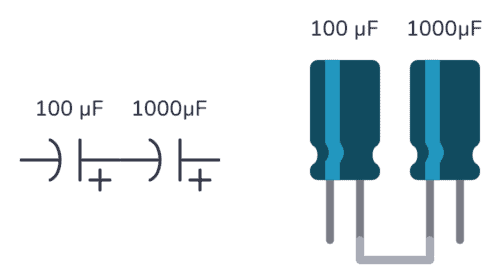
Let’s say you have a 100 µF capacitor in series with a 1000 µF capacitor. What is the total capacitance of those two?
You can use the formula from above and just enter the values, like this:
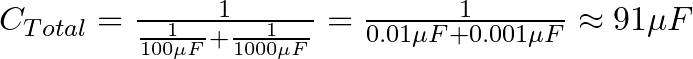
This means the capacitance of these two capacitors in series is 91 µF.
Voltage Across Capacitors in Series
The voltage across capacitors connected in series will be divided between the individual capacitors. If you know that there is 5V across all the capacitors, it means that the sum of the voltages across each individual capacitor will be 5V.
But it’s hard to say what the value for each capacitor is since it depends on its capacitance, internal resistance, and how much it’s been charged.
This isn’t specific to capacitors. Any series connection of components will have the total voltage divided among the components. I recommend reading up on the basics of voltage and current if you’re not comfortable with this concept.
Why Use Capacitors Connected in Series?
The most common reason for connecting capacitors in series among hobbyists is simply that you don’t have the exact capacitor value needed. By connecting several capacitors in series, you can achieve other values.
Let’s say you have built the blinking light circuit, and find that the LED is blinking too slowly. You used 100μF for C1 in the schematic below, and that’s the only value you have in your component kit.
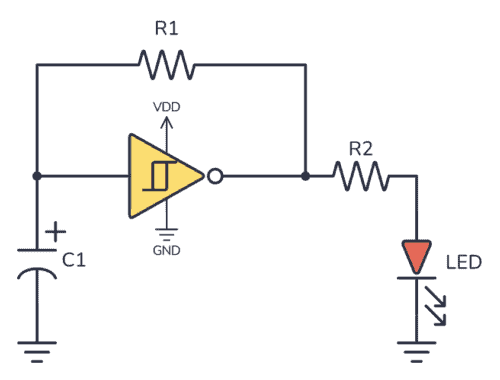
By adding another 100 µF in series with C1, the total resistance becomes 50 µF. And your light blinks with twice the speed instead.
Normally, you never need capacitors connected in series unless you need to achieve a capacitance value that you don’t have at hand.
Summary
The formula for calculating the value of capacitors in series becomes easier if you use the same value for all capacitors. Then the result becomes the value of one, divided by the number of capacitors. Ex five 1000 µF capacitors in series become 1000 µF / 5 = 200 µF.
You usually only place capacitors in series if you need a specific value that you don’t have available.
More Capacitors Tutorials

Get Our Basic Electronic Components Guide
Learn how the basic electronic components work so that circuit diagrams will start making sense to you.
